定义:在一个无向图中,定义一条边覆盖的点为这条边的两个端点。找到一个边集S包含最多的边,使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。S的大小叫做图的最大匹配。
二分图的最大匹配算法:设左边集合为A集合,有边集合为B集合。二分图最大匹配常用的有两种方法。
(1)第一种方法叫做匈牙利算法。这个方法依次枚举A中的每个点,试图在B集合中找到一个匹配。对于A集合中一点x,假设B集合中有一个与其相连的点y,若y暂时还没有匹配点,那么x可以和y匹配,找到;否则,设y已经匹配的点为z(显然z是A集合中的一个点),那么,我们将尝试为z找到一个除了y之外的匹配点,若找到,那么x可以和y匹配,否则x不能与y匹配。
我们以下图为例说明匈牙利匹配算法。
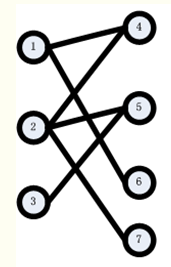
step1:从1开始,找到右侧的点4,发现点4没有被匹配,所以找到了1的匹配点为4 。得到如下图:
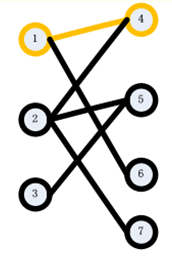
step2:接下来,从2开始,试图在右边找到一个它的匹配点。我们枚举5,发现5还没有被匹配,于是找到了2的匹配点,为5.得到如下图:
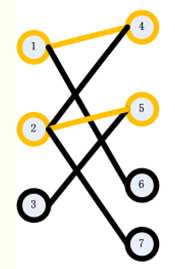
step3:接下来,我们找3的匹配点。我们枚举了5,发现5已经有了匹配点2。此时,我们试图找到2除了5以外的另一个匹配点,我们发现,我们可以找到7,于是2可以匹配7,所以5可以匹配给3,得到如下图:
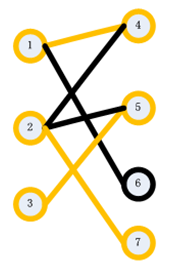
此时,结束,我们得到最大匹配为3。
(2)第二种方法叫做Hopcroft-Karp算法。这个算法大致思想与第一个方法相同。不同之处在于,这个方法每次找到一组互不相交的增广路径。我们用下面的例子说明。
step1:我们从所有未找到增广路径的点,也就是1,2,3,4开始,找增广路径,我们找到了1->2,3->3两条(左边的红线表示增广路径),然后沿着这些增广路径求匹配点,得到了右边的图,即1匹配2,3匹配3。
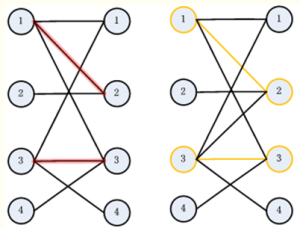
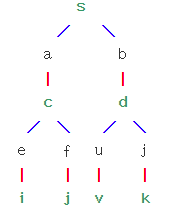
一般图的最大匹配算法:我们从一个没有匹配的节点s开始,使用BFS生成搜索树。每当发现一个节点u,如果u还没有被匹配,那么就可以进行一次成功的增广,即s匹配u;否则,我们就把节点u和它的配偶v一同接到树上,之后把v丢进队列继续搜索。我们给每个在搜索树上的点一个类型:S或者T。当u把它的配偶v扔进队列的时候,我们把u标记为T型,v标记为S型。于是,搜索树的样子是这样的:
否则,我们找到了一个长度为奇数的环,如下图所示

就要进行一次“缩花”的操作!所谓缩花操作,就是把这个环缩成一个点。这个图缩花之后变成了5个点(一个大点,或者叫一朵花,加原来的4个点):缩点完成之后,还要把原来环里面的T型点统统变成S型点,如下图

无向图最大匹配实现:
1 #define MAXN 250 2 3 class GraphMaxMatch 4 { 5 private: 6 int que[MAXN],queHead,queTail; 7 bool g[MAXN][MAXN]; 8 bool inque[MAXN],inblossom[MAXN]; 9 int match[MAXN],pre[MAXN],S[MAXN]; 10 int n; 11 12 void addQueEle(int u) 13 { 14 if(inque[u]) return; 15 inque[u]=1; 16 que[queTail++]=u; 17 if(queTail==MAXN) queTail=0; 18 } 19 int popQueEle() 20 { 21 int u=que[queHead++]; 22 if(queHead==MAXN) queHead=0; 23 return u; 24 } 25 26 int findancestor(int u,int v) 27 { 28 int visit[MAXN]; 29 memset(visit,0,sizeof(visit)); 30 while(1) 31 { 32 u=S[u]; 33 visit[u]=1; 34 if(match[u]==-1) break; 35 u=pre[match[u]]; 36 } 37 while(1) 38 { 39 v=S[v]; 40 if(visit[v]) break; 41 v=pre[match[v]]; 42 } 43 return v; 44 } 45 void reset(int u,int root) 46 { 47 int v; 48 while(u!=root) 49 { 50 v=match[u]; 51 inblossom[S[u]]=1; 52 inblossom[S[v]]=1; 53 v=pre[v]; 54 if(S[v]!=root) pre[v]=match[u]; 55 u=v; 56 } 57 } 58 59 void contract(int u,int v) 60 { 61 int root=findancestor(u,v); 62 memset(inblossom,0,sizeof(inblossom)); 63 reset(u,root); reset(v,root); 64 if(S[u]!=root) pre[u]=v; 65 if(S[v]!=root) pre[v]=u; 66 for(int i=1;i<=n;i++) if(inblossom[S[i]]) 67 { 68 S[i]=root; 69 addQueEle(i); 70 } 71 } 72 73 bool BFS(int start) 74 { 75 for(int i=1;i<=n;i++) pre[i]=-1,inque[i]=0,S[i]=i; 76 queHead=queTail=0; 77 addQueEle(start); 78 while(queHead!=queTail) 79 { 80 int u=popQueEle(); 81 82 for(int v=1;v<=n;v++) if(g[u][v]&&S[v]!=S[u]&&match[u]!=v) 83 { 84 if(v==start||match[v]!=-1&&pre[match[v]]!=-1) 85 { 86 contract(u,v); 87 } 88 else if(pre[v]==-1) 89 { 90 pre[v]=u; 91 if(match[v]!=-1) addQueEle(match[v]); 92 else 93 { 94 u=v; 95 while(u!=-1) 96 { 97 v=pre[u]; 98 int tmp=match[v]; 99 match[u]=v;100 match[v]=u;101 u=tmp;102 }103 return true;104 }105 }106 }107 }108 return false;109 }110 public:111 /**112 vertexNum: vertex number113 G[1~vertexNum][1~vertexNum]: edge relation114 */115 vector > calMaxMatch(116 int vertexNum,const bool G[MAXN][MAXN])117 {118 n=vertexNum;119 for(int i=1;i<=n;i++)120 {121 for(int j=1;j<=n;j++) g[i][j]=G[i][j];122 }123 memset(match,-1,sizeof(match));124 for(int i=1;i<=n;i++) if(match[i]==-1) BFS(i);125 126 vector > ans;127 for(int i=1;i<=n;i++)128 {129 if(match[i]!=-1&&match[i]>i)130 {131 ans.push_back(make_pair(i,match[i]));132 }133 }134 return ans;135 }136 };